số phức chính là những giá trị nằm trong không gian 2 chiều . Số thực là những giá trị trong không gian 1 chiều.
0
6 Câu trả lời
Best Answer
Số thực có thể được hình dung là những giá trị trong không gian 1 chiều, còn số phức chính là những giá trị nằm trong không gian 2 chiều gồm: trục thực và trục ảo
Best Answer
Số thực có thể được hình dung là những giá trị trong không gian 1 chiều, còn số phức chính là những giá trị nằm trong không gian 2 chiều gồm: trục thực và trục ảo
Best Answer
Số thực là một khái niệm cơ bản trong toán học, đại diện cho các số không có phần ảo. Số thực bao gồm tất cả các số từ âm vô cùng đến dương vô cùng và cả các số trên đường thẳng số.
Ví dụ về số thực là 0, -3, 2.5, √2, π (pi), e, ...
Số phức là một khái niệm mở rộng của số thực, bao gồm cả phần ảo. Một số phức bao gồm một phần thực và một phần ảo, biểu diễn dưới dạng a + bi, trong đó a là phần thực và bi là phần ảo (i là đơn vị ảo với tính chất i^2 = -1).
Ví dụ về số phức là 3 + 2i, -4i, 1 - i√3, ...
Số phức có nhiều ứng dụng trong toán học và các lĩnh vực khác nhau, bao gồm điện tử, điện lực, điện tử, cơ học lượng tử và lý thuyết tín hiệu. Các phép toán trên số phức bao gồm cộng, trừ, nhân, chia, và có thể được biểu diễn trên mặt phẳng phức, trong đó trục thực là phần thực và trục ảo là phần ảo.
Best Answer
Số thực có thể hiểu là những giá trị trong không gian 1 chiều, còn số phức chính là những giá trị nằm trong không gian 2 chiều gồm: trục thực và trục ảo
Best Answer
số phức chính là những giá trị nằm trong không gian 2 chiều . Số thực là những giá trị trong không gian 1 chiều.
Best Answer
Số phức là gì? Số thực có thể được hình dung là những giá trị trong không gian 1 chiều, còn số phức chính là những giá trị nằm trong không gian 2 chiều gồm: trục thực và trục ảo.
Điểm khác giữa số phức và số thực
Tự nhiên thêm đơn vị ảo i vào làm chi không biết (=__=), làm ta rất khó hình dung nếu chỉ nhìn cách biểu diễn con số phức và các công thức tính toán của nó. Nào ta hãy cùng biểu diễn / visualize con số phức đó lên không gian 2 chiều (mặt phẳng) cho dễ tưởng tượng nhé!
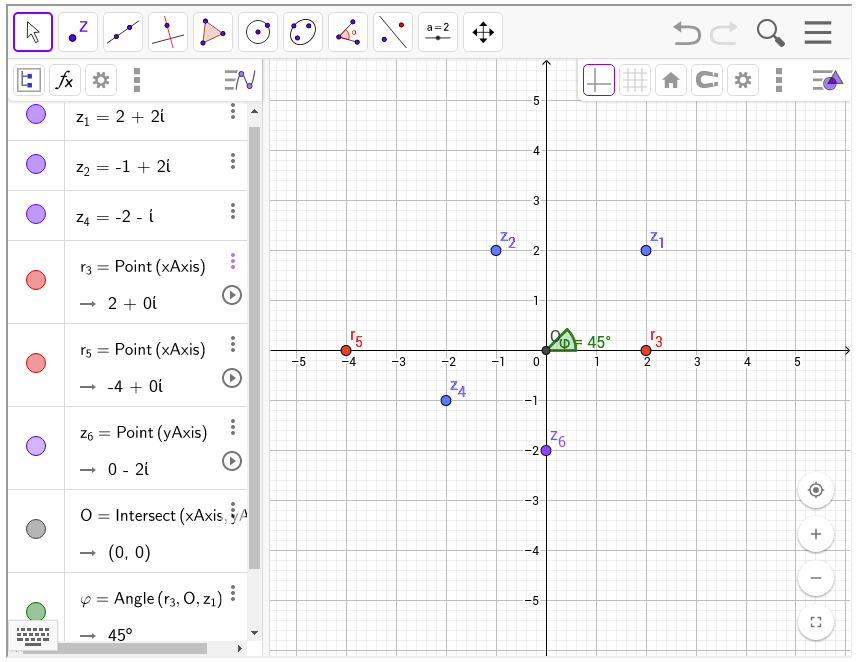
Như hình minh họa trên, trục x (trục hoành) biểu diễn cho phần thực, còn trục y (trục tung) biểu diễn cho phần ảo. Những con số thực mà ta tính toán trước kia sẽ giống như r3
, r5được biểu diễn như trên hình trong không gian phức.
(z6)2=(0−2i)2=(−2i)2=4i2=4(−1)=−4=r5Dạng lượng giác của số phức
z=r(cosφ+isinφ)=rcosφ+r∗i∗sinφ
với r là 1 số thực, φ
là góc.
So sánh với định nghĩa, ta thấy rằng:
- Phần thực: a=rcosφ
Điểm đặc biệt là số phức ở dạng lượng giác được biểu diễn theo độ dài vector (r) và góc của vector (φ
).
Xem Z là điểm có tọa độ (rcosφ,rsinφ)
.Thật vậy: |−−→OZ|=√(rcosφ)2+(rsinφ)2=√(r2((cosφ)2+(sinφ)2)=√(r2(1)=rGóc tạo bởi OZ và Ox là:
arctan(ZyZx)=arctan(rsinφrcosφ)=arctan(tanφ)=φVới ví dụ hình minh họa ở mục trên, số phức z1=2+2i
sẽ được biểu diễn ở dạng lượng giác là: r=√22+22=2√2 φ=arctan(22)=π4 z1=2√2(cosπ4+isinπ4)